-
힙 & 힙 정렬 (heap sort)
-
힙 heap
- 현재 개발된 가장 작은 자료구조들 중 하나
- 이진 트리의 일종으로 이진 트리에 어떤 특성을 부여한 것 (아래에서 이진 트리 binary tree 검색)
- 힙을 통해 '힙 정렬’과 '우선순위 큐priority queue’를 구현
-
이진 힙 구조의 정의
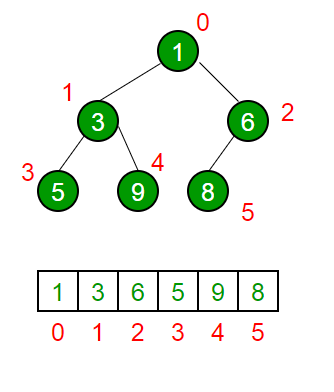
- 배열(array) 구조이면서, 완전 이진 트리로 시각화 가능
- 인덱스 0이 루트
- 왼쪽부터 다음 인덱스의 노드를 채워감 (완전 트리)
- 트리의 사이즈를 n이라고 했을 때, n/2+1부터 n까지의 노드는 모두 단말 노드(leaf)
- 특정 노드의 인덱스 i에 대해서
- root of tree는 first element (i = 1)
- parent(i) = i/2
- left(i) = 2i
- right(i) = 2i + 1
- 특정 노드로 찾아가기 위해서는 어떻게 할까?
- 찾고자 하는 인덱스 i를 2로 계속 나눔
- 마지막 으로 나눈 몫을 제외하고, 나온 나머지를 역순으로 나열
- 루트 노드에서 0이면 왼쪽, 1이면 우측으로 이동!
- ex) 11 -> 0, 1, 1 이렇게 나머지가 역순으로 나오고, 루트 노드에서 좌, 우, 우 노드를 찾아가면 됨!
-
힙 연산 heap operations
- build_max_heap
- 정렬되지 않은 배열을 최대 힙 구조로 바꿈
- n/2 부터 1번 루트 노드까지 각 레벨에서 반복적으로 max_heapify를 진행 (= n/2-1부터 0루트 노드)
- n/2+1부터 n까지의 노드는 모두 트리의 리프(leaf, 단말 노드)로 원소가 한 개인 힙이므로 최대 힙화를 할 필요 X
- 빌드 방식
- naive build 방식: 시간 복잡도 O(n log N) (n번 자료 삽입, 삽입 복잡도는 logN이라서)
- alternative 방식: 시간 복잡도 O(N) (최악의 경우 상승 침투는 n번, 하강 침투의 횟수는 상수에 수렴하므로 결국 O(N))
- 슈도코드
Build_Max_Heap(A) # 배열 A A의 힙 사이즈 = A의 길이 for i = [A의길이/2] down to 1 Max-Heapify(A, i)- max_heapify (최대힙화)
- 서브트리와 서브트리의 루트에서 최대 힙 특성을 위반하는 오류를 ‘하나’ 수정
- 그 오류를 제외하고 나머지는 최대 힙의 특성을 가지고 있다고 가정!
- heap-size를 알아야 함
- 오류를 가진 노드(즉, 최대 힙의 특성을 위반하는 노드)를 아래 서브트리의 노드와 바꿈(하강 침투) → 반복
- 시간 복잡도: O(log N)
- 슈도코드
- build_max_heap
Max_Heapify(A, i) # 배열A와 인덱스i l = left(i) r = right(i) if (l ≤ A의 힙 사이즈) and (A[l] > A[i]) largest = l else largest = i if (r ≤ A의 힙 사이즈) and (A[r] > A[largest]) largest = r if largest ≠ i exchange A[i] with A[largest] Max_Heapify(A, largest) -
'자료구조&알고리즘' 카테고리의 다른 글
| 컴퓨터 과학, 자료구조, 알고리즘 with C언어 (0) | 2022.11.27 |
|---|---|
| 크래프톤정글 2주차; 중위 표기식과 후위 표기식, 스택으로 계산기 구현 (1) | 2022.11.09 |
| 크래프톤정글 2주차; 자료구조 中 스택, 큐, 우선순위 큐 (0) | 2022.11.06 |
| 크래프톤정글 2주차; 이분탐색, 분할정복 (0) | 2022.11.06 |
| 크래프톤정글 1주차; 알고리즘, 재귀함수, 정렬, 완전탐색 (0) | 2022.11.06 |